Raster Based Polygon Packing (CSCE 645)
This project is on github: Link
This was my project for CSCE 645 fall 2021. It was to develop a raster based packing algorithm for 2D polygons in the context of a machine shop (ex. doing layouts and nesting for laser cutting). Of course, this is already a pretty well studied problem (for CPU algorithms). For me this was just a chance to get to revisit GPU programming in a full on project. I knew from the beginning that this almost certainly wouldn't replace that of the existing algorithms (ex. Deepnest), but I was hoping it would at least come close. As it turns out, doing very few but productive calculations is much better than doing an absolute ton of calculations, even if you can do them very very fast.
The architecture was to represent parts and the sheet as a bitgrid (2D bit map). Using bitwise operators, it would be possible to compute if a part collided by checking the bitmasks. Packing these into a 32 bit integer (on which a GPU can perform instruction in single clock cycles) and separating across thousands of threads, you can do collision checks on massive areas at arbitrary resolution in very little time (in theory). All the challenge is how to leverage the GPU's behavior in an efficient manner.
The TL;DR is that while things kinda worked, it never worked right. It was too much to tackle in about 8 weeks, especially with other courses and jobs. The code showed promise, but crashed very frequently. It never had a successful output. But I got what I wanted out of it which was an excuse to try GPU programming on a substantial project. And on that front I learned quite a bit.
General Process for Computing Collisions
What follows is the various writing elements produced for the coursework (fall 2021). They explore/justify this project in the context of a hypothetical contract manufacturing company. They are presented as written for the course, editorialized only to remove duplicate sections.
Proposal
For this project, I propose the development and implementation of a two-round raster based two dimensional polygon packing system. This system is modeled for a theoretical production workflow based on Contract Manufacturing principles (a.k.a. Manufacturing as a Service). In this theoretical model, the manufacturer offers the service of two-dimensional sheet operations, such as CNC Routing. The manufacturer provides this service turn-key, where the customer uploads parts directly and receives physical parts sometime in the future. To offer this service at a competitive cost, the manufacturer must minimize waste of the stock material. Likewise the manufacturer must quickly and accurately price contracts.
These objectives of maximizing packing efficiency while also minimizing overhead time (and monetary) costs is a difficult problem. To solve the time problem, a massively parallel approach can be taken. However, constructing massively parallel systems comes with large initial costs for specialized hardware and ongoing costs for (likely significant) power consumption. In fact, it would be possible to develop a formula which relates power consumption, packing efficiency, and packing time, allowing one the be quantified in terms of the others.
However, there is a significantly cheaper alternative for constructing massively parallel arrays: Graphics Processing Units (GPUs). For example, the Nvidia RTX 3070 contains 5888 CUDA Cores, roughly equivalent to 5888 threads of execution. These cores are less powerful than a standard processor, but their sheer quantity more than makes up the difference. Assuming no memory limitations, this processor could sample 92 square inches at 8 dpi resolution by assigning one sample to each of the cores. The RTX 3070 is clocked at 1.50 GHz with 8 GB of GDDR6 RAM all at 220W of power consumption. This is a powerful device readily available at a low cost of $499.00.
Returning to our contract manufacturing company. The GPU accelerated packing solves our time and costs constraints. However, an efficient packing is still of utmost importance. There exists some literature in this area; see the literature review section for more information. At a high level, there is still room for improvement, which is one key focus for this project. While this is a hard problem to solve, there exists an equally important problem: that of the user interface. While the GPU is a relatively common piece of hardware, it is not assumed to be ubiquitous or available for this purpose. Therefore, the contract manufacturer, wishing to provide the best service, offers the packing on dedicated GPUs. This cloud packing farm would be similar in design and function to that of a render farm in which the service provided manages a group of resources (GPUs) to serve client requests in a managed, scalable, and transparent manner. Additionally this service would need to be secure and reliable, the latter being of particular note in light of Facebook’s recent outage.
What
The project can be divided into two parts. First the packing algorithm. There are packing algorithms, and there are GPU accelerated packing algorithms. See the literature review section for a more through discussion. I am going to focus on a subset of the packing problem which is formalized in the following way. The problem is a derivative of the NP-Hard two-dimensional Bin Packing Problem. In this problem two dimensional polygons, called parts, are packed into one or more larger two-dimensional bounding polygon, called sheets, so that the total number of sheets is minimized. These sheets can represent the available raw material from which to cut parts or machine work volume on which to cut parts. The parts can be regular or irregular, convex or concave. The parts may be rotated within the 2D plane to allow for better packing, but cannot be flipped. Finally, the parts may have interior holes (or concave regions) into which other parts can nest.
There exists some software, both open source and commercial, that can perform these calculations for some/all subsets of this problem. The open source variants run on the CPU in a single or lightly threaded manner. These implementations will provide a benchmark for packing efficiency and time taken for the new algorithm.
For the new algorithm, the expected workflow is to be raster based. We can convert the part polygons into a raster based representation where black pixels (with value 0) are not filled and white pixels (with value 1) are filled. Placing a polygon in the bin involves sliding the mask of the part polygon over the bin (much like a kernel convolution in image processing). As this is a greedy algorithm, there is much significance in the ordering of the parts for placement. This is discussed more in the literature review.
The second portion of this project focuses on migrating the prior portion to a simulated production environment. This is accomplished by distributing the algorithm across multiple compute nodes. Here there is potential for quite a few interesting area of work. First, serving contracts in a maximally efficient manner: can multiple nodes work concurrently to complete a contract in better time or with better efficiency. Alternatively, a scheduler for assigning contracts to nodes in a way to maximize node efficiency.
Goals
- Part 1: An efficient GPU Packing algorithm
- Find or generate test part polygons and test contracts either in a random manner or from some pre-constructed dataset.
- Develop/Implement an algorithm for packing arbitrary, irregular polygons in 2D space, informed by prior work
- Benchmark this algorithm against the existing a open source packing algorithms based principally on time and secondarily on efficiency.
- Quantify the exchange between efficiency cost and time cost.
- Part 2: A scalable Packing Farm
- Develop a distributed system for organizing packing nodes into a larger service.
- Nodes should be able to cleanly enter and leave the pool, but crashes of the node and the scheduler are not expected.
- Service contract in a timely and reliable manner.
- Stretch Goals:
- A Proper Polygon based GPU accelerated implementation
- Multi-node collaboration for contract efficiency
- Multi-node scheduling for resource efficiency
- Nice user interface for the Packing Farm
The literature review and citations were removed for brevity. The are available on GitHub
Project Update 1
The work is proceeding largely according to plan. I spent more time than intended working with various geometric model types. For example, I scanned my hard drives and located approximately 6,000 3D models of various formats. Some, but not all, of these files are items that could be laser cut (i.e. are principally 2D shapes with a constant thickness). I decided that it was really important that I used these real-world files for this project; as opposed to randomly generating 2D polygons. This was an excellent learning opportunity; I've become very familiar with manipulating and converting various 3D file formats: SolidWorks Part (sldprt), Autodesk Inventor Part (.ipt), and STL files. I also developed a simple algorithm for determining if an arbitrary STL is a 2.5D part, and getting the corresponding 2D polygon (including with holes). This polygon representation can be exported to a SVG (for working with existing CPU-Based packing solutions) and with can be converted to a Raster representation (for use with my system).
After this, I wrote a quick and dirty CPU based packer that utilizes an OpenCV hack to determine valid placements. I represent the sheet as all white pixels and the raster as all white pixels (the empty/holey regions are represented as black). Then I perform a template match over the sheet with the raster masked with the raster. This looks for a matching shape/size region that is all white and ignores the black parts of the raster. When a valid placement is found, the raster is XOR'ed with the sheet, turning the taken positions to black. This is a rather slow function, but it was quick to write and has an optional GPU acceleration. However, I probably will not explore this: the template matching will look for all positions that the raster fits and thus inherently will always do quite a bit of extra work. Time is better spent moving directly forward, rather than forward-ish.
The focus now is to take the raster representation and write a more efficient, GPU (CUDA) backed, algorithm. One point of concern is the visibility of the results. Up to this point, I have been working in Python 3.9. I have many good visualization functions, and will probably continue to call them to generate graphics. The question is the GPU (CUDA C/C++) interface with these functions. It is conceptually possible to use Python bindings to call appropriate C/C++: NumPy, a popular C based library for numeric computing in Python. Python bindings is also something that I want to explore so if it is easy enough, it will happen.
Things are moving at a comfortable pace. The focus of the next few weeks is to focus on the GPU based acceleration.
Project Update 2
TLDR: things work; things do not work wellFirst things first, I really didn't have the time and dedication to work on this as much as I would have liked. The past month has been busy both with school and otherwise. However, I did manage to find some time to setup and write an initial version of the GPU-backed packing algorithm. It works; it will return a result, eventually. However, it does not work well. In fact, when factoring in the copying time, it is probably worse than a CPU-only method. There are several reasons for this.
The problem as designed is, roughly, to do an image convolution, such as a Gaussian blur. A shocking discovery was that there is no built-in CUDA utility to perform this natively. Fortunately there are plenty of open-source implementations of this process. However, there are two key differences between our algorithm here and a true image convolution
- A normal image convolution is small, usually acting on 3x3 to 9x9 region of an image. My "convolution" would act on a roughly 16x500 region. This is too big to be done efficiently with a single thread for the convolution. Thus, both the image and the convolution need to be partitioned across multiple GPU threads.
- A convolution is run over the whole image; the packing can stop after the first valid placement is found.
Together, these two factors motivate the development of a custom and optimized packing algorithm. And here is where things get crazy. There are multiple competing constraints that need to satisfied and that are all competing with one another:
- A single thread is very weak, many threads are very strong.
- There is a limit of GPU threads in a GPU block (this limit is 1024).
- There is fast software cache shared memory per-block. It is really really fast, but also limited. Using the maximum number (1024) of threads per block may require more global memory accesses, which is slow.
- This shared memory has a unique structure that requires certain access patterns for maximum performance.
- Global memory requires certain access patterns for maximum performance.
- There is (formally) no synchronization between GPU blocks. Attempting to implement synchronization may deadlock the entire process.
- It is possible to synchronize within a block.
- Starting and stopping multiple blocks is slow. Ideally, the blocks produce an answer before exiting. Also, starting and stopping blocks will complicate the shared per-block memory and may require re-fetching from global memory.
- Copying between CPU (RAM) and GPU is slow. Ideally, all the packing should occur exclusively on the GPU.
All of these are design constraints that define solutions and performance. Writing a robust algorithm for doing so is challenging. The memory access patterns is hard enough, coupled with the lack of inter-block synchronization.
I have ideas for next steps. I also fortunately have more time now to test them. Really the next several weeks is for working on refining this algorithm. There are also simple auxiliary items to do. Right now the workflow requires running several python scripts and manually copying the results around. Likewise, I do not have a good output visualizer to generate graphics quickly and easily.
Final Report
As in Update 2, things work; they do not work wellStones Left Unturned
I never got around to the farm part of the project. Its a combination of not having enough time and not really wanting to after a similar project in another class. There is certainly a benefit, both in terms of addressing the delay with respect to a single packing operation and with respect to multiple concurrent packing operations. Its interesting but time is up and thus will not be happening.
Key Findings (Takeaways)
- CPU Based Packing (Minkowski Sums and other proprietary solutions) is pretty efficient
- High Resolution rasters grow with something between O(n^2) and O(bad); they become untenable very quickly
- GPU Programming is a infinite rabbit hole of nonsense
- They can be really fast though
Workflow Discussion
The workflow happens in roughly three parts
- Preprocessing - converting to our raster format
- Packing - GPU based
- Postprocessing - Manual Based
In the preprocessing step, I convert arbitrary 3D files into my raster format. My format is a bitwise mapping of the part. There is a header row of part width, height, and rasterized DPI. This can be significantly compressed into a binary file but for ease I left them uncompressed in ASCII. An Example is shown below.
File example removed for brevity
I pulled the source files from various engineering projects. These were converted to STL via the Autodesk Inventor API. Then I used a python script to convert STL files to SVG files. This was done in two rounds. The first was to attempt to determine if the part was principally 2d. That is if the file had two primary "faces" that were parallel and perpendicular to all other faces it could be considered to be two dimensional. For these objects, I obtained their SVG representation by projecting the STL edges to one of the parallel planes and selecting the ones that formed an exterior boundary (based on the number of times they appear). This was not necessary to the packing procedure and in reality was largely a distraction. But it was fun to write.
The SVG was represented using the library `Shapely`. This was then run through `Rasterio` to produce a `Numpy` array representing the part (which is then used to generate the disk file). All of these libraries are C-binding exposed in python and run orders of magnitude faster than my attempts at writing the same code.
GPU Packing step is discussed in depth in a later section
The GPU Code, when working, produces a list of placements for the polygons. Ideally, this would automatically generate some usable output representation. At the moment it simply puts the output to console and figures are generated by hand.
GPU Programming Introduction
in briefThe GPU is a very powerful piece of computing hardware. The key component is the streaming multiprocessor. Where a normal computer CPU (single core) operates on two pieces of data in a single cpy cycle, the streaming multiprocessor acts on multiple pairs of data at once. This is referred to a Single Instruction Multiple Data (SIMD). In the case of the Nvidia CUDA architecture, the multiprocessor can act on 32 pairs of data per instruction cycle.
These sets of 32 threads are called warps. Warps live in a Block. Blocks live in a Grid. Blocks have a small cache of shared memory but most of the memory is global, shared among all components of a Grid. Blocks are unordered and should operate completely independent of all other blocks.
The execution of a function over a Grid is referred to as a Kernel.
There are two key components to GPU programming:
- Memory access is in mod32 blocks by register address. For example, it is not possible for both register `0x01` and register `0x21` to be read concurrently.
- There is no synchronization between blocks. There is also no officially supported way to yield the multi-processor. Thus while you _can_ implement software synchronization with any one of the supported atomic operators, doing so almost certainly leads to deadlocks.
For the remainder of this document I am going to discuss with respect to the __Nvidia GeForce GTX 1060__. I picked this GPU Because it was what I had. It is a PCI 3.0x16 GPU at a base clock of around 1500 MHz, 6 GB GDDR5 memory. It has 10 streaming multi processors. It was first released in August 2016 and uses the Pascal Micro-architecture.
I also will also briefly mention the current top of the line GeForce GPU, the __Nvidia GeForce GTX 3090__. The relevant statistics are list below.
| Name | Base Clock | CUDA Cores | Streaming Multiprocessors | Architecture |
|---|---|---|---|---|
| GTX 1060 | 1500MHz | 1280 | 10 | Pascal |
| GTX 3090 | 1400 MHz | 10496 | 82 \[1] | Ampere |
\[1] Third Party Data
GPU Implementation Details
Within the GPU processing code there are three GPU Kernels (functions) required for the packing process.
The first takes a part raster and a sheet (also a raster) and builds an output raster representing the colliding and free spaces. This is the most complex and will be discussed more later.
The second Kernel takes the output raster and does a strided reduce to efficiently determine the best placement. For the sake of testing, the best placement is the one which results in the furthest left and down placement. This is the first place where inter-block synchronization comes into play. We need to know when all blocks can produce an output so we can reduce across blocks. This is a non-trivial problem. One solution is to launch a sub kernel (which I could not get to compile). Another is to use some global atomic operations, however this is problematic because you need to atomically update both an X and Y value. Finally, control can be returned to CPU and it can handle the final reduction step. This incurs an overhead on the order of milliseconds which is acceptable at the moment.
The final Kernel bakes the part into the sheet so that future Kernels will mark colliding. This segments the sheet into blocks in X and Y and, for those blocks that overlap with the part's placement, does a bitwise or between the part and the sheet.
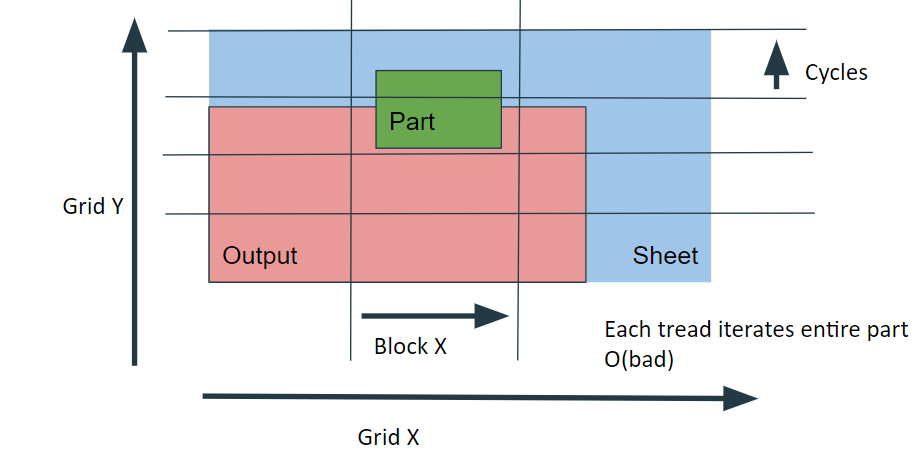
Returning now to the first Kernel. The output raster (which is inherently smaller than the sheet) is segmented into X and Y coordinates. The collision details for a fixed portion of the output is determined over the entire part and sub-portion of the sheet that the part collides with. Thus inside each output thread, there is still O(n^2) scan over the part. Effectively, there is up to O(n^4) collisions to check. This is problematic.
There are a couple trivial optimizations that could be applied. First, once the part collides in one position, there is no need to check any additional possible collisions of the part. This provides a significant speedup. Additionally, if the sheet region is completely empty, there is no need to check for the collisions. This provides a significant speedup while the sheet is mostly empty.
GPU Theoretical Behavior
Ignoring the the real world, the GPU is a very powerful component. For this research we are concerned principally with bit operations. These are fast, happening in a single clock cycle. Therefore, calculating the theoretical performance (without memory delays or bus conflicts) per clock cycle is as simple as:
- _Number Streaming Multi Processors_ * _# Resident Warps_ * 32 _(Threads per warp)_ * 32 _(Bits per integer)_
And per second the prior formula times the clock rate. The number of bit-level computations performed per second. For our two example GPUs are:
- GTX 1060: $1.966E15$ bit comparisons per second
- GTX 1060: $1.966E15$ bit comparisons per second
Depending on your sampling resolution, you can convert this to a square inches number:
| Name | 300 DPI | 600 DPI | 1000 DPI | 10000 DPI |
| GTX 1060 | $2.185E10$ | $5.461E9$ | $1.966E9$ | $1.999E7$ |
| GTX 3090 | $1.672E11$ | $4.180E10$ | $1.505E10$ | $1.505E8$ |
Or In terms of football fields (including endzones):
| Name | 300 DPI | 600 DPI | 1000 DPI | 10000 DPI |
| GTX 1060 | $2.634E+03$ | $658.4$ | $237.0$ | $2.370E$ |
| GTX 3090 | $2.016E+04$ | $5.039E+03$ | $1.814E+03$ | $18.14$ |
Once the real world is taken into consideration, this number reduces _by many orders of magnitude_. Additionally, it is not as simple as checking if a part can go in _A_ place, but rather checking if a part can go in _ALL_ places.
GPU Actual Behavior and Future Work Directions
$1.665E7$ DPI per Second (currently, RTX 1060), or about $1000$ sq in per second.
I used 170 DPI. This is because I wanted a sheet of 24in x 48in and at 170 DPI the sheet requires 128 x 255 32bit registers, which seemed like a nice number.
It takes about 1 second to calculate all the collisions of the part (4 seconds without trivial optimizations).
It takes about 100us to bake a part into the sheet.
It takes about 40us to determine the first free space.
Ignoring the collision map generation for the moment, the algorithm is quite fast. There is some overhead in copying to and from the device but overall insignificant compared to that of the collisions calculations. However, there is still some relatively simple design choices that can be applied. The first is transitioning to device primary compute. If all the parts were loaded to the GPU before the kernel launches, there is no need to return to the CPU. Moreover, the kernel could run asynchronously, allowing the CPU to do other tasks. This is part of Dynamic Parallelism (see later) which I could not make work.
Another optimization is the computation of reflections and rotations on the GPU device. It should be a relatively fast operation, on the order of baking the part. If coupled with a device primary architecture, would allow the entire process to run efficiently completely within the single device.
Handling an arbitrary sheet size is trivial; take the starting sheet and mask off the region that is used. Additionally, this could be used to mask off holes or other items that cannot be included in any part, allowing for greater yield on damaged sheets.
Dynamic Parallelism provides the greatest potential for improvement. This is the process of intelligently allocating more threads and kernels to regions with more detail. Effectively this is some form of recursive quad-tree-esque branching. Since most of the space is either densely full with parts or empty without parts, this is a potential major performance improvement.
Dynamic Parallelism Api Principles: https://developer.nvidia.com/blog/cuda-dynamic-parallelism-api-principles/
Tensor cores may provide another area of potential improvement. If the decision herein can be modeled as a tensor operation, the specialized tensor cores will likely provide better performance. However, one key problem exists with the architecture of the tensor cores: they are designed for floating point operations. I do not know if they support integer bitwise operations, but do not recall seeing them at any point in the documentation.